Luke Singham

How to Make a Churn Model in R

The following post details how to make a churn model in R. It was part of an interview process for which a take home assignment was one of the stages. The company stated this should take 2hrs, which is entirely unrealistic. To minimise the time cost, my analysis is very succinct and short on the exploratory analysis and amount of models compared. The churn model got me to the final stage, however little in the way of feedback was offered. There is considerable debate in the tech industry as to whether take home exams are a fair assessment or even a reasonable ask on an individual. My assessment is that this is a lazy way to interview and a very high cost on the interviewee. If you really want to work for a particular company, then sure you might be prepared to do what it takes. I doubt I will do another take home assignment.

The analysis was done in Rmarkdown and the output copied into this blog post following these helpful pointers. If you would like to play with the data and full unabridged code please visit this github repo.

Aim #

  1. Please create a model that predicts which businesses are likely to churn at the start of 2015 based on the vertical and incorporation_date.
  2. We have an inkling that a dropoff in the number of mandates added might be an advance indicator of someone churning. Please can you assess whether this might be true, and if you think it is useful, incorporate it into your model from part (1).
# Load packages
suppressPackageStartupMessages({
    library(data.table)   # Fast I/O
    library(dplyr)        # Data munging
    library(tidyr)        # Data munging
    library(lubridate)    # Makes dates easy
    library(plotly)       # Interactive charts
    library(magrittr)     # pipe operators
    library(caret)        # Handy ML functions
    library(rpart)        # Decision Trees
    library(rpart.plot)   # Pretty tree plots
    library(ROCR)         # ML evaluation
    library(e1071)        # Misc stat fns
    library(randomForest) # rf
})

set.seed(42)

# Read data and drop row number column
df <- fread("monthly_data_(2)_(2).csv", drop = 1)

# Have a glimpse of the data
glimpse(df)
## Observations: 902
## Variables: 27
## $ company_id          <int> 4, 5, 6, 7, 8, 10, 11, 12, 13, 14...
## $ 2014-01-01_payments <dbl> 8, 0, 2, 3, 0, 0, 0, 0, 0, 0, 4, ...
## $ 2014-02-01_payments <dbl> 4, 0, 2, 3, 0, 0, 0, 2, 0, 11, 1,...
## $ 2014-03-01_payments <dbl> 7, 39, 1, 1, 6, 0, 0, 0, 8, 0, 1,...
## $ 2014-04-01_payments <dbl> 7, 0, 3, 7, 50, 1, 0, 0, 2, 0, 0,...
## $ 2014-05-01_payments <dbl> 1, 54, 1, 4, 119, 0, 1, 0, 0, 0, ...
## $ 2014-06-01_payments <dbl> 2, 0, 2, 1, 151, 3, 0, 0, 0, 0, 2...
## $ 2014-07-01_payments <dbl> 2, 0, 2, 7, 182, 0, 0, 0, 3, 0, 0...
## $ 2014-08-01_payments <dbl> 4, 22, 1, 2, 167, 0, 0, 0, 2, 0, ...
## $ 2014-09-01_payments <dbl> 3, 0, 1, 5, 180, 0, 0, 0, 0, 9, 5...
## $ 2014-10-01_payments <dbl> 5, 0, 2, 8, 157, 1, 0, 0, 0, 2, 1...
## $ 2014-11-01_payments <dbl> 5, 0, 1, 2, 105, 0, 0, 0, 0, 0, 0...
## $ 2014-12-01_payments <dbl> 9, 0, 3, 8, 57, 0, 0, 0, 0, 0, 0,...
## $ 2014-01-01_mandates <dbl> 0, 4, 0, 0, 0, 4, 4, 0, 0, 22, 0,...
## $ 2014-02-01_mandates <dbl> 0, 31, 1, 0, 2, 3, 8, 0, 0, 20, 1...
## $ 2014-03-01_mandates <dbl> 0, 24, 0, 0, 0, 5, 19, 0, 0, 11, ...
## $ 2014-04-01_mandates <dbl> 53, 18, 0, 1, 0, 0, 0, 0, 1, 11, ...
## $ 2014-05-01_mandates <dbl> 0, 8, 0, 0, 0, 0, 0, 0, 1, 15, 0,...
## $ 2014-06-01_mandates <dbl> 0, 7, 0, 0, 0, 0, 0, 0, 0, 13, 5,...
## $ 2014-07-01_mandates <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 13, 16...
## $ 2014-08-01_mandates <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 14, 8,...
## $ 2014-09-01_mandates <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 16, 2,...
## $ 2014-10-01_mandates <dbl> 0, 0, 0, 0, 1, 0, 0, 0, 0, 16, 1,...
## $ 2014-11-01_mandates <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 6, 0, ...
## $ 2014-12-01_mandates <dbl> 0, 0, 0, 3, 0, 0, 0, 0, 0, 11, 0,...
## $ vertical            <chr> "gym/fitness", "freelance d...
## $ incorporation_date  <chr> "2003-09-25", "2008-10-22", ...

Data Munging #

Some data munging needs to occur for our binary classifiers to make use of the data within. This includes handling dates.

# Reshape data and create new columns
df %<>%
    gather(key = date, value = quantity, starts_with("20")) %>%
    separate(date, c("date","paymentMandate"), "_") %>%
    spread(paymentMandate, quantity) %>%
    mutate(
      incorporation_date = as.Date(incorporation_date),
      date = as.Date(date),
      incorporation_time = round(
        as.numeric(difftime(as.Date("2014-12-01"),
        as.Date(incorporation_date),
        unit="weeks")) / 52.25,
        digits = 1)
    ) %>%
    arrange(date)

# What does the new data look like?
glimpse(df)
## Observations: 10,824
## Variables: 7
## $ company_id         <int> 1, 2, 3, 4, 5, 6, 7, 8, 10, 11, 12, 13, 14,...
## $ vertical           <chr> "gym/fitness", "gym/fitness", "freelance de...
## $ incorporation_date <date> 2013-05-30, 2003-09-25, 2008-10-22, 2005-0...
## $ date               <date> 2014-01-01, 2014-01-01, 2014-01-01, 2014-0...
## $ mandates           <dbl> 1, 0, 0, 0, 4, 0, 0, 0, 4, 4, 0, 0, 22, 0, ...
## $ payments           <dbl> 0, 1, 6, 8, 0, 2, 3, 0, 0, 0, 0, 0, 0, 4, 4...
## $ incorporation_time <dbl> 1.5, 11.2, 6.1, 9.4, 1.2, 9.1, 4.0, 2.9, 1....

What is Churn #

For the purposes of this project I have defined ‘churn’ as zero mandates and payments for the first instance of that after the last mandate/payment made.

# Create binary 'churn' column
df$churn <- 0

# For use in for loop - upper bound of data
max.date <- max(df$date)

# Mark all companies as churned in the month immediately their last activity
for (company in unique(df$company_id)) {

    # Subset data to company
    df.sub <- subset(df, df$company_id == company)

    # Index of last positive mandate OR payment
    last.pos.idx <- tail(which(df.sub$mandates != 0 | df.sub$payments != 0), 1)

    # Get date of last activity
    last.activity.date <- df.sub$date[last.pos.idx]

    # If less than max.date of dataset mark churn ELSE do nothing i.e. positive at end of period
    if (last.activity.date < max.date) {

        # Get churn date (last positive month plus 1mth)
        churn.date <- last.activity.date %m+% months(1)

        # Mark month of churn as 1
        df[df$date == churn.date & df$company_id == company, ]$churn <- 1
    }
}

# Multiple rows per company, filter for last month or churn month values...
# Get churners
df %>% filter(churn == 1) -> churners

# Get max date row of remainers (non-churners)
df %>%
    filter(churn == 0 & !(company_id %in% churners$company_id) & date == max(date)) -> remainers

# Combine and variables coded ready for modelling
churners %>%
    rbind(remainers) %>%
    mutate(vertical = as.factor(vertical),
           churn    = as.factor(churn)) -> model.df

Churns over the year #

# Plot churners
model.df %>%
    filter(churn == 1) %>%
    group_by(date) %>%
    summarise(n = n()) %>%
    plot_ly( x = ~date, y = ~n, type = 'scatter', mode = 'lines')

Could do more on exploratory but this is the easiest to cut back for this report.

Balance of the data #

The proportion of churn is 32.04%. Representing an imbalanced dataset. Accuracy is an inappropriate measure (I could get 67.96% accuracy predicting no businesses leave), so I will focus on recall and accuracy.

# Loyal vs Churn
table(model.df$churn)
##
##   0   1
## 613 289

Model #

Survival models and binary classifiers are common approaches to ‘Churn’ models. I will approach the model using the latter, though if I had more time I would investigate other classifiers and a survival model. I will limit the range of models to a logistic, a decision tree and an ensemble.

Split Data #

# 80/20 train test split
index    <- createDataPartition(model.df$churn, p = 0.8, list = FALSE)
train.df <- model.df[index, ]
test.df  <- model.df[-index, ]

# Check balance of the training split
table(train.df$churn)
##
##   0   1
## 491 232
# Check balance of the test split
table(test.df$churn)
##
##   0   1
## 122  57

Logistic #

# Run model
Logistic.model <- glm(churn ~ incorporation_time + vertical,
                      data   = train.df,
                      family = binomial(link = 'logit'))

# Predict
log.pred <- predict(Logistic.model, newdata = test.df, type = 'response')

# Convert probs to binary
log.pred <- as.factor(ifelse(log.pred > 0.5, 1, 0))

# Evaluation Metrics
log.result    <- confusionMatrix(data = log.pred, test.df$churn)
log.precision <- log.result$byClass['Pos Pred Value']
log.recall    <- log.result$byClass['Sensitivity']
log.F1        <- log.result$byClass['F1']

Decision Tree #

# Train model
tree.model <- rpart(churn ~ incorporation_time + vertical,
                    data = train.df,
                    method = "class",
                    control = rpart.control(xval = 10))

# Plot
rpart.plot(tree.model)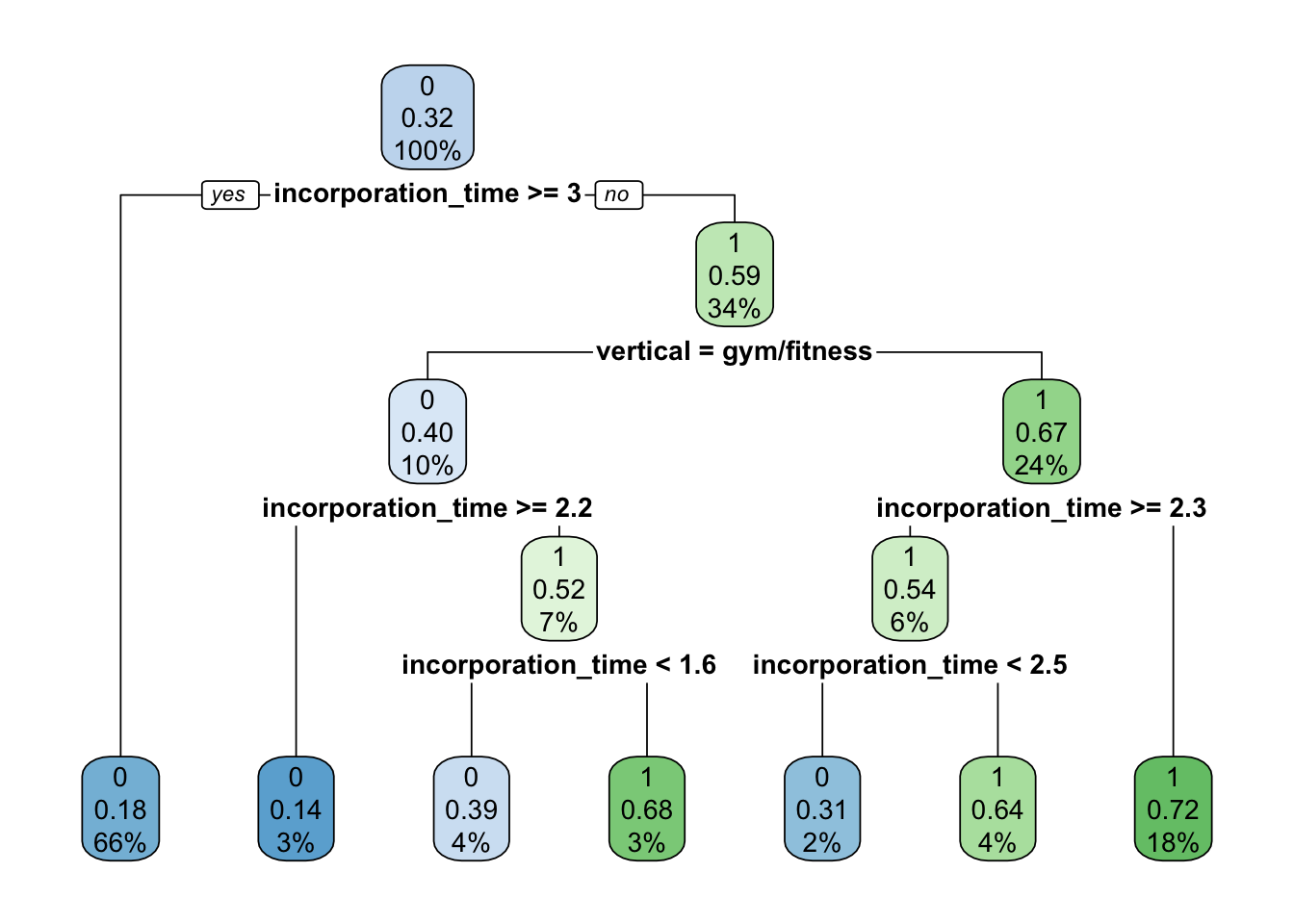

# Evaluation metrics
tree.pred      <- predict(tree.model, newdata = test.df, type = "class")
tree.result    <- confusionMatrix(data = tree.pred, test.df$churn)
tree.precision <- tree.result$byClass['Pos Pred Value']
tree.recall    <- tree.result$byClass['Sensitivity']
tree.F1        <- tree.result$byClass['F1']

Random Forest (Ensemble) #

# Train model
forest.model <- randomForest(churn ~ incorporation_time + vertical,
                       data = train.df,
                       ntree=200,
                       type="classification")

# See error reduction with number of trees ( not much gained beyond ~25 trees)
plot(forest.model)

# Look at the variable Importance from the random forest
varImpPlot(forest.model, sort = T, main="Variable Importance")

# Evaluation metrics
forest.pred      <- predict(forest.model, newdata = test.df, type = "class")
forest.result    <- confusionMatrix(data = forest.pred, test.df$churn)
forest.precision <- forest.result$byClass['Pos Pred Value']
forest.recall    <- forest.result$byClass['Sensitivity']
forest.F1        <- forest.result$byClass['F1']

Evaluation Metrics #

log.precision;
## Pos Pred Value
##      0.8333333
tree.precision;
## Pos Pred Value
##      0.8088235
forest.precision;
## Pos Pred Value
##      0.8134328
log.recall;
## Sensitivity
##   0.9016393
tree.recall;
## Sensitivity
##   0.9016393
forest.recall;
## Sensitivity
##   0.8934426
log.F1;
##        F1
## 0.8661417
tree.F1;
##        F1
## 0.8527132
forest.F1;
##        F1
## 0.8515625

Surprisingly, the logistic regression model performs the best, with the top precision score and equal recall score with that of the decision tree. With more time, I’d see if tweaks to the decision tree and random forest models could change this. Its also possible over/undersampling could help. From here on I will use the logistic regression model.

Examine the incorporation of time information #

Per the second aim, examine the inclusion of time information. This requires more data munging. Taking code used from above, I will extend to include the derivation of a very basic time period variable.

# Create binary 'leading_indicator' column
model.df$leading_indicator <- 0

# Min date for which a leading_indicator can be calculated (lower limit of data)
min.date <- min(df$date)

# If month before 'churn' (churn-1), is below the level of mandates of the month 2 months prior (churn-2) then
# make leading_indicator == 1
for (company in churners$company_id) {

    # Subset data to company
    df.sub <- subset(df, df$company_id == company)

    # Get month prior to churn
    month.prior <- df.sub$date[df.sub$churn == 1] %m-% months(1)

    # Get two months prior to churn
    two.month.prior <- df.sub$date[df.sub$churn == 1] %m-% months(2)

    # If two months prior is within dataset date range and level of mandates is greater than 0
    if ((two.month.prior > min.date) && (df.sub$mandates[df.sub$date == two.month.prior] > 0)) {

        # Compare number of mandates 1 month prior to 2 months prior, if less, mark 'leading_indicator' as '1'
        if (df.sub$mandates[df.sub$date == month.prior] < df.sub$mandates[df.sub$date == two.month.prior]) {
            model.df[model.df$company_id == company, ]$leading_indicator <- 1
        }
    }
}

Of the churners, how many have a leading indicator? #

model.df %>%
    filter(churn == 1) %>%
    group_by(leading_indicator) %>%
    summarise(n=n()) %>%
    mutate(percent = round(n / sum(n) * 100, 1))
## # A tibble: 2 x 3
##   leading_indicator     n percent
##               <dbl> <int>   <dbl>
## 1                 0   264    91.3
## 2                 1    25     8.7

Re-train model and evaluate #

# Re-split data so 'leading_indicator' is in columns (the index remains the same)
train.df <- model.df[index, ]
test.df  <- model.df[-index, ]

Logistic #

# Run model
lead.logistic.model <- glm(churn ~ incorporation_time + vertical + leading_indicator,
                      data   = train.df,
                      family = binomial(link = 'logit'))

# Predict
log.pred <- predict(lead.logistic.model, newdata = test.df, type = 'response')

# Convert probs to binary
log.pred <- as.factor(ifelse(log.pred > 0.5, 1, 0))

# Evaluation Metrics
lead.log.result    <- confusionMatrix(data = log.pred, test.df$churn)
lead.log.precision <- log.result$byClass['Pos Pred Value']
lead.log.recall    <- log.result$byClass['Sensitivity']
lead.log.F1        <- log.result$byClass['F1']

Evaluation Metrics #

Compare the precision and recall of the logistic model with and without the lead_indicator.

log.precision
## Pos Pred Value
##      0.8333333
lead.log.precision
## Pos Pred Value
##      0.8333333
log.recall
## Sensitivity
##   0.9016393
lead.log.recall
## Sensitivity
##   0.9016393
# Have a look at the model coefficients and p-values
summary(lead.logistic.model)

## Call:
## glm(formula = churn ~ incorporation_time + vertical + leading_indicator,
##     family = binomial(link = "logit"), data = train.df)
##
## Deviance Residuals:
##     Min       1Q   Median       3Q      Max  
## -1.4429  -0.8252  -0.4957   0.9938   2.5564  
##
## Coefficients:
##                              Estimate Std. Error z value Pr(>|z|)
## (Intercept)                   0.74066    0.20007   3.702 0.000214 ***
## incorporation_time           -0.26140    0.03045  -8.584  < 2e-16 ***
## verticalfreelance developer   0.12614    0.21737   0.580 0.561714
## verticalgym/fitness          -0.91099    0.22342  -4.077 4.55e-05 ***
## leading_indicator            18.06219  482.97671   0.037 0.970168
##
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
##     Null deviance: 907.42  on 722  degrees of freedom
## Residual deviance: 736.18  on 718  degrees of freedom
## AIC: 746.18
##
## Number of Fisher Scoring iterations: 15

Generally, it is best to minimise the AIC. The Logistic.model model AIC is 800.5 compared with the lead.logistic.model incorporating the lead_indicator is 746.18. The lead_indicator has not changed the predictive power on this dataset, but since the AIC favours a better model fit whilst penalising for additional predictors, the model to choose is the lead.logistic.model.

Re-train model and save #

# Re-train on all data
final.model <- glm(churn ~ incorporation_time + vertical + leading_indicator,
                      data   = model.df,
                      family = binomial(link = 'logit'))

Recommendations for further investigation/Comments #


✍️ Want to suggest an edit? Raise a PR or an issue on Github